|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
| Compare the two quantities and choose the best answer from four choices given. |
1. A quarter is a coin of 25 cents and a dime is a coin of 10 cents.
Quantity A = The number of different combinations of quarters and dimes whose total value is $13.35
Quantity B = 25
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterSince 4 quarters make a dollar, $13.35 requires 53 quarters and 1 dime.
It is not possible to replace a quarter with dimes; however, it is possible to replace 2 quarters with 5 dimes.
The different combinations can be represented by ordered pairs where Q denotes quarters and D denotes dimes as follows:
(53Q, 1D), (51Q, 6D), (49Q, 11D), ..., ..., (1Q, 131D).
So, there are 27 different combinations.
2. For any positive integer n,
S(n) is defined as the sum of all the positive integers < n and
E(n) is defined as the sum of all the positive even integers < n.
Quantity A = S(12)
Quantity B = E(25)/2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterS(12) = 1 + 2 + 3 + ... + 10 + 11
E(25)/2 = (2 + 4 + 6 + ... + 22 + 24)/2 = 1 + 2 + 3 + ... + 11 + 12
3. 2y + 3z = 27
3z − 2y = 27
Quantity A = z
Quantity B = 9
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalAdding the two equations gives 6z = 54 or z = 9.
4. y > 0
Quantity A = y
Quantity B = The positive square root of y
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The relationship cannot be determined from the information givenIf y = 1, then Quantity A equals Quantity B.
If y > 1, then Quantity A is greater, e.g., if y = 4, then Quantity A = 4 and Quantity B = 2.
If y < 1, then Quantity B is greater, e.g., if y = 1/4, then Quantity A = 1/4 and Quantity B = 1/2.
5.

Diagram is illustrative and is not drawn to scale.
The total area of the four identical small circles equals the area of the colored region.
Quantity A = Radius of the large circle
Quantity B = Diameter of the small circle
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterLet the radius of the large circle be R and the radius of each of the four small circles be r.
Total area of four identical small circles = 4 (π r2).
Area of colored region = π R2 − 4 (π r2).
Since these areas are equal, π R2 − 4 π r2 = 4 π r2 or π R2 = 8 π r2.
Thus, R = √8 r = √2 (2r) = 1.414 (diameter of the small circle).
6.
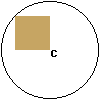
A circle of radius r has its center at C.
Quantity A = The area of the colored square
Quantity B = 0.5r2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalLet a be the length of the side of the square.
Area of colored square = a2.
The diagonal of the square is the radius of the circle.
By Pythagoras' Theorem, a2 + a2 = r2 or 2 a2 = r2.
Area of colored square = a2 = 0.5r2.
7. Quantity A = 5/6
Quantity B = (5/6)4
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterOne could use the calculator. Then, 5/6 = 0.833
(5/6)4 = (5 x 5 x 5 x 5)/(6 x 6 x 6 x 6) = 625/1296 = 0.482
It is worth noting that if 0 < y < 1, then yn will always be less than y for n > 1.
8. p < q < r < s < 0
Quantity A = pq
Quantity B = rs
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterNote that p, q, r and s are negative.
Let p = −8, q = −5, r = −3 and s = −1.
Then, pq = 40 and rs = 3.
In fact, pq is always greater than rs in this case.
9. Quantity A = The area of a rectangle whose perimeter is 24
Quantity B = The area of a rectangle whose perimeter is 36
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The relationship cannot be determined from the information givenLet l be the length of the rectangle and b its breadth.
Then, Perimeter of rectangle = 2 (l + b) and Area of rectangle = l b.
If perimeter (of rectangle A) = 24, then l + b = 12. Let l = 11 and b = 1, then area = 11. On the other hand, if l = 7 and b = 5, then area = 35.
If perimeter (of rectangle B) = 36, then l + b = 18. Let l = 10 and b = 8, then area = 80. On the other hand, if l = 17 and b = 1, then area = 17.
So, Quantity B is greater if area of rectangle A is 11 and area of rectangle B is 80. On the other hand, Quantity A is greater if area of rectangle A is 35 and area of rectangle B is 17.
10. All of Debbie's crayons are red, green or blue. One-eighth of Debbie's crayons are blue. Debbie has thrice as many blue crayons as red crayons.
Quantity A = The total number of blue and red crayons
Quantity B = The number of green crayons
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterLet C be the total number of crayons.
Number of blue crayons = C/8.
Number of red crayons = C/24.
Number of blue and red crayons = (C/8) + (C/24) = (3C +C)/24 = 4C/24 = C/6.
Number of green crayons = C − (C/6) = 5C/6.
11. Quantity A = (1/3) + (1/6) + (0.2)2
Quantity B = (1/2) + 0.04
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equal(1/3) + (1/6) = (2/6) + (1/6) = 3/6 = 1/2
Also, (0.2)2 = 0.2 x 0.2 = 0.04
12. The Los Angeles office has 12 employees whereas the New York office has 25 employees. In each office, the number of male employees is greater than the number of female employees.
Quantity A = The number of male employees in the Los Angeles office
Quantity B = The number of male employees in the New York office
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterThe number of male employees in the New York office is 13 or more (i.e., more than half of 25), which is greater than the total number of employees in the Los Angeles office (which is 12).
13. The sides of a triangle are 5, 12 and z.
Quantity A = z
Quantity B = 18
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterIt is important to note that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
So, 5 + 12 > z or z < 17.
Also, 5 + z > 12 or z > 7.
So, 7 < z < 17.
14. David earned a 70 on each of his first two tests, an 80 on his third test, and a 75 on each of the fourth and fifth tests.
Quantity A = David's average after three tests
Quantity B = David's average after five tests
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterIf David had earned a 70 on each his first three tests, his average would have obviously been 70. But, he earned 10 marks more in his third test, so his average after three tests will be 73.33 (i.e., 70 + 10/3).
Since David gets a 75 on each of the fourth and fifth tests (which is higher than 73.33), he will end up with a higher average after five tests.
A quick way to compute the average after five tests (which is not necessary) is to use the method followed earlier. Taking 70 as the reference, David earned 10 marks more in his third test, 5 marks more in his fourth test, and 5 marks more in his fifth test. So, his average after 5 tests would be 74 (i.e., 70 + 20/5).
Note that the average (arithmetic mean) of n numbers is their sum divided by n.
15. Five fair coins are tossed.
Quantity A = The probability of getting two heads
Quantity B = The probability of getting three heads
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalThis problem can be solved without actually calculating the probabilities. The probability of getting three heads in five coin tosses is the same as the probability of getting two tails. Further, by a symmetry argument, the probability of getting two heads is identical to the probability of getting two tails.
16. Quantity A = 5859 + 5959
Quantity B = 6060
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greater5859 + 5959 < 5959 + 5959 = 2 (5959) < 59 (5959) = 5960 < 6060.
Note your calculator will give an error message because the numbers are too big.
The only other alternative is to use the method of induction (or reason by analogy) as follows.
12 + 22 = 4 which is less than 33 = 27.
23 + 33 = 35 which is less than 44 = 256.
17. Line A passes through (1,4) and (3,2). Line B is perpendicular to line A.
Quantity A = The slope of line A
Quantity B = The slope of line B
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterBecause lines A and B are perpendicular,
(slope of line A) x (slope of line B) = −1.
Slope of line A = (2 − 4)/(3 − 1) = −1.
So, slope of line B = 1.
Alternatively, a quick sketch will show that line A is sloping downwards and has a negative slope. A line perpendicular to it will slope upwards and have a positive slope.
18. The regular price of a computer system at ABC Store is 20% less than the regular price of the same computer system at XYZ Store.
Quantity A = Price of computer system when ABC Store has 5% off sale
Quantity B = Price of computer system when XYZ Store has 25% off sale
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterLet P be the regular price of the computer system at XYZ Store.
Then, the regular price of the computer system at ABC Store is 0.8 P.
Quantity A = 0.95 (0.8 P) = 0.76 P and Quantity B = 0.75 P.
19. Quantity A = The time it takes to drive 110 miles at 65 miles per hour
Quantity B = The time it takes to drive 130 miles at 55 miles per hour
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterAt 65 miles per hour, it will take less than two hours to drive 110 miles.
At 55 miles per hour, it will take more than two hours to drive 130 miles.
It is not necessary to actually compute the time using the formula:
Time = Distance/Speed.
Quantity A = 110/65 < 2 hours and Quantity B = 130/55 > 2 hours.
20. Quantity A = (541/3)/3
Quantity B = 2/(41/3)
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalTaking the cube of Quantity A gives 54/(33) = 54/27 = 2.
Taking the cube of Quantity B gives (23)/4 = 8/4 = 2.
21. Quantity A = The circumference of a circle whose diameter is 37
Quantity B = The circumference of a circle whose radius is 19
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterA circle whose radius is 19 has a diameter equal to 38. A circle with a larger diameter will have a larger circumference, because circumference C is proportional to diameter D (note C = π D).
22. y < 0
Quantity A = −3y
Quantity B = y3
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterWhen y is negative, −3y is necessarily positive and y3 is necessarily negative, e.g., when y = −2, −3y = 6 and y3 = −8.
23. The area of a circle equals the area of a square.
Quantity A = The circumference of the circle
Quantity B = The perimeter of the square
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterLet the area of the square be a2. Then, the side of the square equals a, and the perimeter of the square equals 4a.
Now, area of circle = a2 = π r2 where r is the circle's radius.
So, Circumference of circle = 2 π r = 2 π (a/√π) = 2 √π a = 3.545 a.
24. The number of cubic inches in the volume of a cube is twice the number of square inches in its surface area.
Quantity A = The length of an edge of the cube
Quantity B = 3
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterIf a is the length of an edge of the cube, then
volume = a3 and surface area = 6a2.
Now, a3 = 2 (6a2) or a = 12.
25. Each edge of a wooden cube is 4 inches. It is painted blue. Then it is cut into 64 small cubes. Each edge of these small cubes is 1 inch.
Quantity A = The number of small cubes with exactly one blue face
Quantity B = The number of small cubes with exactly two blue faces
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalA little visualization with a sketch may help solve this problem.
There are 8 small cubes with no blue faces (the 2" x 2" x 2" core of the 4" cube).
There are 24 small cubes with one blue face (4 each at the center of each of the 6 faces of the 4" cube).
There are 24 small cubes with two blue faces (2 each at the center of each of the 12 edges of the 4" cube).
There are 8 small cubes with three blue faces (at the corners of the 4" cube).
Try the Quiz : GRE Test Prep : Quantitative Comparison VII
|