Math : Trigonometry |
| Formats | Worksheet / Test Paper | Quiz | Review |
|
Hide all answers View all answers Print Try the Quiz 1. 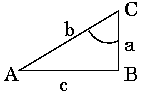 For the figure given on the left, the value of sin C is For the figure given on the left, the value of sin C is• c / b • a / b • b / a • a / c • c / a Answer: c / b The sine of an angle is defined as Opposite Side / Hypotenuse. Now for angle C, the opposite side is c and the hypotenuse is b. Hence the correct answer is c/b. 2. From the figure given on the right, the value of sin A + cos A is 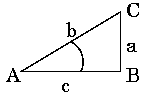 • (b + c)/a • (a + b)/c • (a + c)/b • (a - b)/b • (a + b + c)/b Answer: (a + c)/b We know sin A = a/b, and cos A = c/b. Hence sin A + cos A = (a + c)/b. 3. 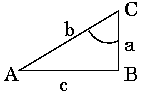 From the figure given on the left, the value of cos C is From the figure given on the left, the value of cos C is• b / a • c / a • c / b • b / c • a / b Answer: a / b We know that cos of any angle = Base/Hypotenuse. Now for the angle C, the base is a and hypotenuse is b. So cos C = a/b.
4. For the figure given on the right, which of the following relationships is true : 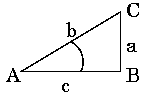 • sin A = a / c • cos A = b / c • cot A = c / a • tan A = a / b • sec A = b / a Answer: cot A = c / a By definition, cot A = 1 / tan A = c / a. 5. 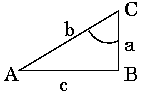 From the figure given on the left, the value of cos C + sin A is From the figure given on the left, the value of cos C + sin A is• b/a + a/b • a/b + c/b • 2a/b • 2b/a • b/c + c/a Answer: 2a/b The value of cos C = a/b. Similarly the value of sin A = a/b. Hence cos C + sin A = 2a/b. 6. Which of the following relationships is true: • sin A / cos A = tan A • sin A / cosec A = cot A • cos A / sin A = sec A • cosec A / sin A = cos A • tan A / cot A = sin A Answer: sin A / cos A = tan A The expression sin A / cos A = tan A is a useful one to remember in trigonometry. 7. tan A / sin A = • cosec A • sin A • cos A • sec A • 1 / sin A Answer: sec A tan A = sin A / cos A. Therefore tan A / sin A = 1 / cos A = sec A. 8. (sin A / tan A) + cos A = • 2 sec A • 2 cos A • sec A • 2 cosec A • 1 + cos A Answer: 2 cos A We know tan A = sin A / cos A. Therefore (sin A / tan A) + cos A = cos A + cos A = 2 cos A. 9. cot A tan A = • sin A • 1 • cos A • sin A cos A • 1/(sin A cos A) Answer: 1 cot A = 1 / tan A. Hence cot A tan A = 1. Alternatively cot A = cos A/sin A and tan A= sin A/cos A. So cot A tan A = (cos A/sin A) (sin A/cos A) = 1. 10. 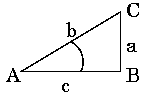 From the figure, the value of cosec A + cot A is From the figure, the value of cosec A + cot A is• (a + b)/c • a/(b + c) • b/(a + c) • (a + c)/b • (b + c)/a Answer: (b + c)/a We know cosec A = b/a and cot A = c/a. Hence cosec A + cot A = (b + c)/a. 11. Which of the following relationships is true: • sin A cot A = 1 • sin A + cosec A = 1 • sec A - cos A = 1 • sec A cot A = 1 • cos A sec A = 1 Answer: cos A sec A = 1 By definition, sec A = 1 / cos A. So cos A sec A = 1 is true. 12. 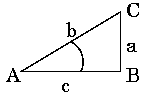 From the figure, the value of sin2 A + cos2 A is From the figure, the value of sin2 A + cos2 A is• a/b + c/b • 1 • b/a + c/b • (a/b + c/b)2 • (b/a + c/b)2 Answer: 1 This question is a bit tricky. We know sin A = a/b and cos A = c/b. So sin2 A + cos2 A = (a2 + c2) / b2. By Pythagoras Theorem, a2 + c2 = b2 for a right-angled triangle. Hence sin2 A + cos2 A = 1, which is a famous identity. 13. 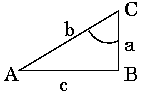 From the figure, the value of cot C + cosec C is From the figure, the value of cot C + cosec C is• (a + c)/b • (c + b)/a • (a + b)/c • a/c + c/b • c/a + b/c Answer: (a + b)/c cot C is Base/Opposite Side and cosec C is Hypotenuse/Opposite Side. From these definitions, the values of cot C and cosec C are given by a/c and b/c respectively. Hence the answer is (a + b)/c. 14. cosec A / sec A = • tan A • sin A • cos A • cot A • sin A + cos A Answer: cot A By definition, cosec A = 1 / sin A and sec A = 1 / cos A. So cosec A / sec A = cos A / sin A = cot A. 15. For the figure given on the right, the value of cot A is 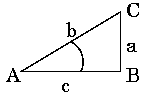 • sin A / cos A • cos C / sin C • a / c • c / b • tan C Answer: tan C The value of cot A is c/a. Similarly the value of tan C is c/a. Hence cot A = tan C.
Try the Quiz : Practice Exercise for Trigonometry Module 1 : Trigonometric Functions |