Example:

Three stars, each of mass m = 84 x 10²⁰ kg, are situated on the vertices of an equilateral triangle of side a = 6 x 10³ km. The only force acting on them is the gravitational force. Due to some cosmic event, all the three stars are simultaneously set in motion. The three stars move in a circle, maintaining their original separation and configuration. Find:

1. the velocity of each star; and
2. the time period of the circular motion.

Solution: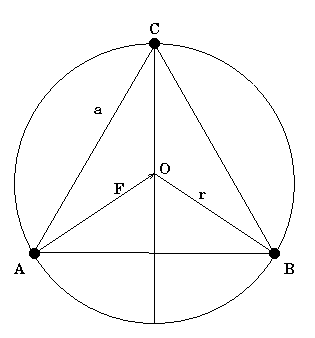

The situation is shown in the schematic diagram above with the three stars labeled A, B and C. Let each star attract the other by a force F'. Then

The resultant force on any star, say A, is

For the circle, the radius r is given by

Assume star A is moving with velocity v. The centrifugal force is balanced by the gravitational force of attraction. A force balance on star A gives

Thus, the velocity of each star is

Substituting G = 6.67 x 10^-11 N m²/kg², m = 84 x 10²⁰ kg and a = 6 x 10⁶ m, the velocity v = 305.58 m/s.

b. The time period T of the circular motion is readily calculated from

Substituting v = 305.58 m/s and r = 3.46 x 10⁶ m, the time period T = 71.22 x 10³ s.