Example:

A point mass m = 50 x 10² kg is placed at the center of the base of a uniform hemisphere of mass M = 169 x 10⁸ kg and radius R = 117 m. What is the potential energy of interaction due to gravitational force?

Solution: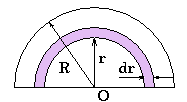

Consider an elementary section of thickness dr at a distance r from the center O of the hemisphere as shown in the figure. Let dM be the mass of this elementary section. Then,

Using equation (G.17) for a distributed mass system, the potential V at the point O is given by

The potential energy of interaction due to gravitational force is the product of the potential V and the mass m. Thus,

Now substituting m = 50 x 10² kg, M = 169 x 10⁸ kg and radius R = 117 m in the expression obtained above, the potential energy of interaction U = - 72.26 J.