Solution:
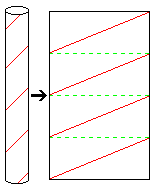
To make visualization easy, it is convenient to conceptually open out the bark of the tree trunk and flatten it. The cylindrical surface will then be a rectangle (as illustrated in the figure alongside for 4 twists of the creeper).
It may be noted that:
Width of the rectangle = Circumference of the cylinder = 32 inches.
Height of the rectangle = Vertical distance on the cylinder = 60 inches (in one twist).
Using the Pythagorean Theorem for a right-angled triangle,
Length of the hypotenuse = (32
2 + 60
2)
1/2 = 68 inches.
Now, the number of twists the creeper makes around the tree trunk is 8 (= 480 / 60).
If the length of the creeper (as given by the hypotenuse) is 68 inches in one twist, then the total length of the creeper in 8 twists is 544 inches.
Food for thought:
Is the total length of the creeper in the above calculation the actual length or the minimum length?