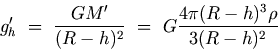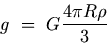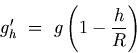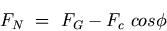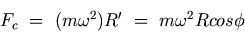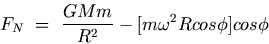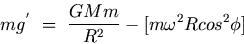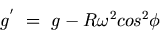College Physics: GravitationG.5 Factors affecting Acceleration due to GravityG.5.1 Altitude
Equation (G.5) when divided by the value of acceleration due to gravity at the Earth's surface (g = GM/R 2) gives
If h is much smaller than R, then equation (G.6) can be rewritten using binomial expansion as
Thus the value of gravitational acceleration decreases as one moves away from the surface of the Earth. Click here for Solved Example G.5: Acceleration due to Gravity at a Height G.5.2 Depth Below the Earth's Surface
Now, acceleration due to gravity at the surface can be written as
Dividing equation (G.8) by equation (G.9), we obtain
The value of gravitational acceleration decreases if one moves towards the center of the Earth, e.g., in mines. Thus, the value of gravity is maximum at the Earth's surface and decreases with increase in height as well as with depth. Click here for Solved Example G.6: Acceleration due to Gravity at a Depth G.5.3 Rotation of the Earth
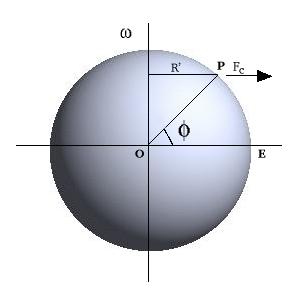
Figure G.1 Effect of the Earth's Rotation on gravitational acceleration. The net force pulling the particle towards the center of the Earth is
where FN is the total force acting on the particle, FG is the force due to gravity and Fc is the centrifugal force. The centrifugal force is given by
On substituting the appropriate expressions in equation (G.11), we obtain
If g' represents the gravitational acceleration, then
Thus the observed value of gravitational acceleration is minimum at the equator and maximum at the poles.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
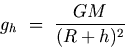
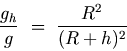
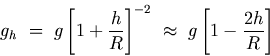
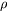 , then
, then