|
Transport Phenomena - Heat Transfer Problem :
Heat conduction from a sphere to a stagnant fluid
Problem.
A heated sphere of diameter D is placed in a large amount of stagnant fluid. Consider the heat conduction in the fluid surrounding the sphere in the absence of convection. The thermal conductivity k of the fluid may be considered constant. The temperature at the sphere surface is TR and the temperature far away from the sphere is Ta.
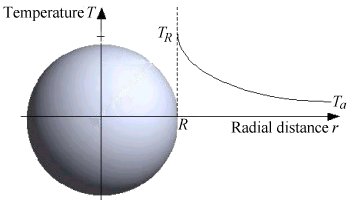 Figure. Heated sphere in a large amount of stagnant fluid.
a) Establish an expression for the temperature T in the surrounding fluid as a function of r, the distance from the center of the sphere.
b) If h is the heat transfer coefficient, then show that the Nusselt number (dimensionless heat transfer coefficient) is given by
Hint: Equate the heat flux at the sphere surface to the heat flux given by Newton's law of cooling.
Solution.
a)
From a heat balance over a thin spherical shell in the surrounding fluid,
where S is the rate of generation of heat per unit volume. In this case, S = 0 in the fluid.
Since the thermal conductivity k for the fluid is constant, on substituting Fourier's law
we get
On integrating,
The integration constants are determined using the boundary conditions:
where R is the radius of the sphere.
On substituting the integration constants, the temperature profile is
b)
Using Fourier's law and differentiating the temperature profile, the heat flux is
Equating the heat flux at the sphere surface (r = R) to the heat flux as per Newton's law of cooling, we get
The Nusselt number (which is the dimensionless heat transfer coefficient) is
where D is the diameter of the sphere.
Note:
- This is a well-known result that is worth remembering. It provides the limiting value of the Nusselt number for heat transfer from a sphere in the presence of convection at low Reynolds and Grashof numbers.
- The Nusselt number Nu must not be confused with the Biot number Bi. Though the two dimensionless groups are similar-looking, they differ as given below.
Related Problems in Transport Phenomena :
Transport Phenomena - Heat Transfer Problem : Forced convection heat transfer for plug flow in circular tube
- Problem of determining Nusselt number for forced convection in cylindrical coordinates
Syvum in other languages: French, Spanish, Portuguese
|
