|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
1. A man is walking along a straight road. He notices the top of a tower subtending an angle A = 60o with the ground at the point where he is standing. If the height of the tower is h = 30 m, then what is the distance (in meters) of the man from the tower?
Answer: 17.32
Solution:  |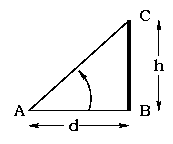
Let BC represent the tower with height h = 30 m, and A represent the point where the man is standing. AB = d denotes the distance of the man from tower. The angle subtended by the tower is A = 60o.
From trigonometry, | tan A = tan 60o = h / d = | √3 |
So d = 30 / √3 s m.
Hence the distance of the man from the tower is 17.32 m. |
2. A little boy is flying a kite. The string of the kite makes an angle of 30o with the ground. If the height of the kite is h = 24 m, find the length (in meters) of the string that the boy has used.
Answer: 48
Solution:  |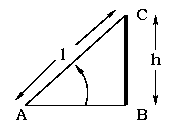
If the kite is at C and the boy is at A, then AC = l represents the length of the string and BC = h represents the height of the kite.
From the figure, sin A = sin 30o = h / l = 1 / 2. Hence the length of the string used by the little boy is l = 2 h = 2 (24) = 48 m. |
3. Two towers face each other separated by a distance d = 15 m. As seen from the top of the first tower, the angle of depression of the second tower's base is 60o and that of the top is 30o. What is the height (in meters) of the second tower?
Answer: 17.32
Solution:  |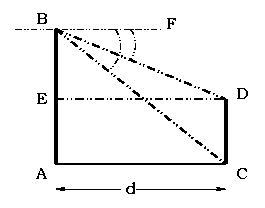
The first tower AB and the second tower CD are depicted in the figure on the left.
First consider the triangle BAC. Angle C = 60o.
tan BCA = tan 60o = AB / AC.
This gives AB = d tan 60o.
Similarly for the triangle BED, BE = d tan 30o.
Now height of the second tower CD = AB − BE
= d (tan 60o − tan 30o)
= 15 (√3 − 1/ √3) = 15 × 2 / √3 = 17.32 m. |
4. A ship of height h = 21 m is sighted from a lighthouse. From the top of the lighthouse, the angle of depression to the top of the mast and the base of the ship equal 30o and 45o respectively. How far is the ship from the lighthouse (in meters)?
Answer: 49.69
Solution:
Let AB represent the lighthouse and CD represent the ship. From the figure, tan BCA = tan 45o = AB / AC.
Similarly for the triangle BED, tan BDE = tan 30o = BE / ED.
Now, AC = ED = d.
Height of the ship = CD
= AB − BE = d (tan 45o − tan 30o) = 21 m.
Thus distance of the ship from the lighthouse d = 21 / (1 − 1 / √3 ) = 49.69 m | |
5. Two men on opposite sides of a TV tower of height 28 m notice the angle of elevation of the top of this tower to be 45o and 60o respectively. Find the distance (in meters) between the two men.
Answer: 44.17
Solution:
The situation is depicted in the figure with CD representing the tower and AB being the distance between the two men.
For triangle ACD,
tan A = tan 60o = CD / AD.
Similarly for triangle BCD,
tan B = tan 45o = CD / DB.
The distance between the two men is AB = AD + DB
= (CD / tan 60o) + (CD / tan 45o)
= (28 / √3) + (28 / 1) = 44.17 m. |  |
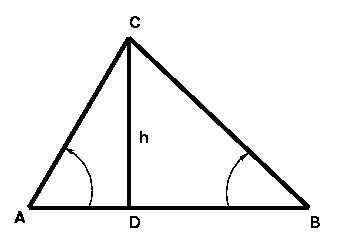6. Two men on the same side of a tall building notice the angle of elevation to the top of the building to be 30o and 60o respectively. If the height of the building is known to be h =60 m, find the distance (in meters) between the two men.
Answer: 69.28
Solution: In the figure, A and B represent the two men and CD the tall building.
tan A = tan 30o = DC / AC = h / AC; and
tan B = tan 60o = DC / BC = h / BC.
Now the distance between the men is AB
= x = AC − BC = (h / tan 30o) − (h / tan 60o)
= (60 √3 ) − (60 / √3 ) = 69.28 m. |  |
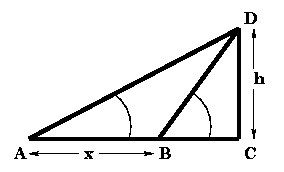7. A pole of height h = 50 ft has a shadow of length l = 50.00 ft at a particular instant of time. Find the angle of elevation (in degrees) of the sun at this point of time.
Answer: 45
Solution:  |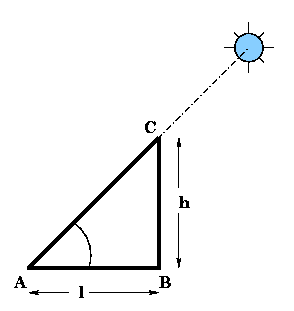
In the figure, BC represents the pole and AB its shadow.
tan A = BC / AB
= h / l = 50 / 50.00 = 1.000
From trigonometric tables, we note that
tan A = 1.000 for A =45o.
Hence the angle of elevation of the sun at this point of time is 45o.
|
8. You are stationed at a radar base and you observe an unidentified plane at an altitude h = 3000 m flying towards your radar base at an angle of elevation = 30o. After exactly one minute, your radar sweep reveals that the plane is now at an angle of elevation = 60o maintaining the same altitude. What is the speed (in m/s) of the plane?
Answer: 57.74
Solution: 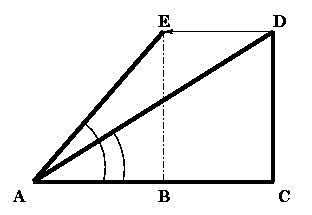 | In the figure, the radar base is at point A. The plane is at point D in the first sweep and at point E in the second sweep. The distance it covers in the one minute interval is DE.
From the figure,
tan DAC = tan 30o = DC / AC = h / AC.
Similarly,
tan EAB = tan 60o = EB / AB = h / AB.
Distance covered by the plane in one minute = DE = AC − AB
= (h / tan 30o) − (h / tan 60o)
= (3000 √3) − (3000 / √3 ) = 3464.10 m.
The velocity of the plane is given by V = distance covered / time taken
= DE / 60 = 57.74 m/s. |
Try the Quiz : Practice Exercise for Trigonometry Module 3 : Word Problems on Heights and Distances
|
