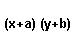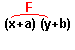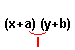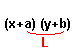| Preparation |
Just what you need to know ! |
How to Expand (x ± a)(y ± b) by FOIL Method ?
(x + a)(y + b) = x(y + b) + a(y + b) = xy + bx + ay + ab
Note that the terms in the first bracket multiply the terms in the second bracket during expansion.
The expansion may also be termed the FOIL method because:
First terms (xy) are multiplied;
Outer terms (bx) are next multiplied;
Inner terms (ay) are then multiplied; and
Last terms (ab) are finally multiplied.
This is illustrated below.
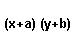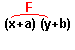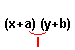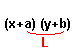
In a similar manner,
(x + a)(y − b) = x(y − b) + a(y − b) = xy − bx + ay − ab
(x − a)(y + b) = x(y + b) − a(y + b) = xy + bx − ay − ab
(x − a)(y − b) = x(y − b) − a(y − b) = xy − bx − ay + ab The FOIL method for multiplying two binomials is nothing but the distributive law. Each term in the first bracket is multiplied by each term in the second bracket and then like terms are combined, if possible.
Example :
(3x − 7)(4x + 9) = (3x)(4x) + (3x)(9) − (7)(4x) − (7)(9) = 12x2 + 27x − 28x − 63
The like terms (27x − 28x) may be combined to finally give
(3x − 7)(4x + 9) = 12x2 − x − 63
Practice Exercise for Algebra Module on Expansion by FOIL Method
|