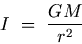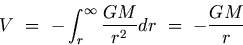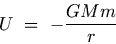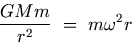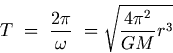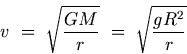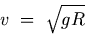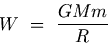Previous Contents Next College Physics: Gravitation G.6 Gravitational Intensity and Potential G.6.1 Gravitational Intensity The gravitational intensity I is defined as the force experienced by a unit mass when placed in the gravitational field of another mass M. From equation (G.3), (G.16) G.6.2 Gravitational Potential The gravitational potential V at a point in the gravitational field is defined as the work done in taking a unit mass from that point to infinity against the force of gravitational attraction. From the definition, we have (G.17) G.6.3 Gravitational Potential Energy The work obtained in bringing a body from infinity to a point in the gravitational field is called the gravitational potential energy of the body at that point. It is represented usually by U and is given mathematically as 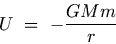(G.18) The gravitational potential energy at infinity is assumed to be zero. Click here for Solved Example G.7: Gravitational Potential Energy G.7 Satellites A satellite is any body revolving around a large heavenly body like a planet. For example, the Moon is a satellite of the Earth. The Moon is a natural satellite. There may even be artificial or man-made satellites revolving round a planet. Consider a satellite of mass m at a distance r from the center of the planet rotating at an angular velocity w. If the mass of the planet is M, then the motion of the satellite is governed by the following force balance. 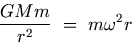(G.19) G.7.1 Time Period of a Satellite The time taken by a satellite to complete one revolution round a planet is called its time period T, and an expression for it can be easily calculated using equation (G.19) as follows. 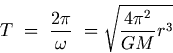(G.20) Equation (G.20) is basically Kepler's Third Law as applied to satellites. G.7.2 Orbital Velocity of a Satellite The orbital velocity v of the satellite is readily obtained from equation (G.19) on using v = w r and g = GM/R 2. Thus, 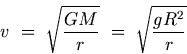(G.21) For the case of a satellite revolving around the Earth in a circle at a height h from the Earth's surface with h much smaller than R, equation (G.21) may be approximated by 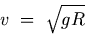(G.22) Click here for Solved Example G.8: Time Periods and Orbital Velocities of Satellites G.8 Escape Velocity The escape velocity of a body is defined as the minimum velocity with which a body must be projected from the surface of the Earth, so that it may not return. The work done in taking a body from the surface of the Earth to infinity is 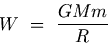(G.23) If a body is to be projected such that it may never return, then its kinetic energy must equal this work done as given below. 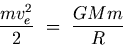(G.24) Thus, the expression for the escape velocity is 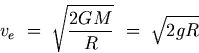(G.25) For the Earth, the value of the escape velocity is 11.2 km/s. Click here for Solved Example G.9: Escape Velocity of a Satellite G.9 Planets The equations derived above for satellites are valid for planets with M representing the mass of the sun (rather than the Earth) and m representing the mass of the planet (rather than the satellite). The sun may be treated as an inertial frame of reference as its mass is several times more than that of the planet. The path of the planets may be assumed to be circular rather than elliptical because the difference in major and minor axes is not much. The greatest difference amongst the nine planets in our solar system is for Pluto which is only 3%.   Previous Contents Next

 

English
Français
Português
Español
Deutsch
日本語
हिन्दी