|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
Is the data given in the two statements, labeled (1) and (2), sufficient for answering the question?
All numbers used are real numbers. |
1. If 16x + y/2 + 1 = 4x + 2y, what are the values of x and y?
(1) 72x + 3y = 4938
(2) 5−4 = 25x − y
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.The question statement gives the following equation, on converting to same base:
42x + y + 2 = 4x + 2y
∴ 2x + y + 2 = x + 2y or y − x = 2
Statement (1) gives the following equation, on converting to same base:
72x + 3y = 776
∴ 2x + 3y = 76
The two equations (y − x = 2 and 2x + 3y = 76) can be simultaneously solved to obtain values of the two unknowns x and y. Thus, statement (1) ALONE is sufficient.
Statement (2) gives the following equation, on converting to same base:
5−4 = 52x − 2y
∴ 2x − 2y = −4 or y − x = 2
Note that this equation is the same as that obtained from the question statement. Thus, statement (2) ALONE is not sufficient.
2. If n is a prime number, what is the value of n?
(1) n < 100 and n + 4 is a multiple of 11.
(2) 71 < n < 77
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) tells us that n = 7, or n = 29, or n = 73. Thus, statement (1) ALONE is not sufficient.
Statement (2) tells us that n = 73. Thus, statement (2) ALONE is sufficient.
Note that the prime numbers are
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...
3. How much did a family spend on their Alaskan vacation?
(1) There were 4 members in the family.
(2) Each family member spent $1799.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) specifies the number of members, but not how much each member spent. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies how much each member spent, but not the number of members. Thus, statement (2) ALONE is not sufficient.
Since the total expenses are obtained on multiplying the number of members by the amount each member spent, BOTH statements TOGETHER are sufficient.
4.
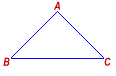
Is Δ ABC isosceles?
(1) AB = AC
(2) ∠ B = ∠ C
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.A triangle is isosceles if two of its sides are equal in length. Thus, statement (1) ALONE is sufficient.
A triangle is isosceles if two of its angles are equal. Thus, statement (2) ALONE is sufficient.
5. Did Company P report a larger increase in monetary losses as compared to Company Q?
(1) Company P reported an increase in losses of 4.5%.
(2) Company Q reported an increase in losses of 7%.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.In this case, the increase in monetary losses (in dollars) cannot be determined for either company from the statements given.
To answer the question, at least one actual numerical value (in dollars) for the losses reported by each company is needed.
Thus, statements (1) and (2) TOGETHER are NOT sufficient.
Mathematically, (P2/P1) − 1 = 0.045 and (Q2/Q1) − 1 = 0.07,
where P1 and P2 are the monetary losses for Company P, whereas Q1 and Q2 are the monetary losses for Company Q. Subscripts 1 and 2 denote two different points in time.
The question asks which is the greater quantity : (P2 − P1) or (Q2 − Q1)?
To answer the question, P1 or P2 must be given. Also, Q1 or Q2 must be given.
6. What is the value of m?
(1) m = √81
(2) m2 = 81
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.Statement (1) tells us that m = 9. Thus, statement (1) ALONE is sufficient.
Statement (2) tells us that m = ±9. Thus, statement (2) ALONE is not sufficient.
7. A numismatist collected coins worth $4 on a particular day. How many nickels did he collect on that day?
(1) He collected 60 coins on that day.
(2) He collected only nickels and dimes on that day.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) specifies the total number of coins, but not the denominations of the different coins. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies that only nickels and dimes were collected, but nothing about their number. Thus, statement (2) ALONE is not sufficient.
But, BOTH statements TOGETHER are sufficient as shown below:
If n is the number of nickels, then (60 − n) is the number of dimes.
Since a nickel is 5 cents and a dime is 10 cents,
5n + 10 (60 − n) = 400.
Solving the above equation for n gives the number of nickels.
8. Susan's flower-vase contains only yellow asters and orange asters. What is the ratio of orange asters to yellow asters in her flower-vase?
(1) The number of yellow asters is 2 less than the number of orange asters.
(2) The number of yellow asters is ¾ the number of orange asters.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.If o and y are the number of orange asters and yellow asters respectively, then o / y is the ratio that is needed.
Statement (1) gives the following equation:
y = o − 2, from which o / y cannot be determined. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives the following equation:
y = ¾ o, which can be solved to obtain o / y = 4/3. Thus, statement (2) ALONE is sufficient.
9. What is the greatest value possible for integer k?
(1) k is a multiple of 4.
(2) k is a factor of 43 × 53 and 4 × 102.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies that k is a multiple of 4, but the multiples of 4 are infinite. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies that k is a factor of 43 × 52 and 4 × 102. The greatest common factor can always be uniquely determined by prime factorization (e.g., 43 × 53 = 26 × 53; 4 × 102 = 24 × 52; greatest common factor = 24 × 52). Thus, statement (2) ALONE is sufficient.
10. If b2 + c2 = 80, what is bc?
(1) c = −2b
(2) b − c = 12
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Statement (1) gives c = −2b, which may be substituted in b2 + c2 = 80 to obtainb2 + 4b2 = 80 or b2 = 16.
If b = 4, then c = −2 x 4 = −8.
If b = −4, then c = −2 x −4 = 8.
In both cases, bc = −32. Thus, statement (1) ALONE is sufficient.
Statement (2) gives c = b − 12, which may be substituted in b2 + c2 = 80 to obtain b2 + (b2 − 24b + 144) = 80 or b2 − 12b + 32 = (b − 4)(b − 8) = 0.
If b = 4, then c = 4 − 12 = −8.
If b = 8, then c = 8 − 12 = −4.
In both cases, bc = −32. Thus, statement (2) ALONE is sufficient.
11.

What is the area of rectangle PQRS?
(1) Its diagonal is 13 feet.
(2) PS = 5 feet
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.To find the area of rectangle, its length and width must be known because
Area of rectangle = Length × Width.
Statement (1) specifies the diagonal. To find the rectangle's area using the Pythagorean theorem, either its length or its width must be known. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the width. To find the rectangle's area, either its length or its diagonal must be known. Thus, statement (2) ALONE is not sufficient.
Knowing the width as well as the diagonal of the rectangle allows us to calculate its length by the Pythagorean theorem, and subsequently its area. Thus, BOTH statements TOGETHER are sufficient.
12. 296 pupils of a school opt for swimming and/or skating as a part of their extra-curricular activities. How many pupils opt for swimming only?
(1) 198 pupils opt for both swimming and skating.
(2) 51 pupils opt for skating only.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.The question statement specifies the total number of pupils (t). Let the number of pupils who opt for swimming only be w, the number who opt for skating only be k, and the number who opt for both swimming and skating be b. Then,
w + k + b = t.
Statement (1) specifies b. Without knowing k, it is notpossible to determine w. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies k. Without knowing b, it is not possible to determine w. Thus, statement (2) ALONE is not sufficient.
Knowing k and b, w can be determined from w = t − k − b. Thus, BOTH statements TOGETHER are sufficient.
13. A rectangular photograph is to be placed in a wooden frame. What is the area of the photograph?
(1) The length of the photograph is 7 inches.
(2) The area of the wooden frame is 55 square inches.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.To find the area of the photograph, its length and width must be known or some additional information about the wooden frame must be given.
Statement (1) specifies the length of the photograph, but not its width. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the area of the wooden frame, but nothing about the photograph. Thus, statement (2) ALONE is not sufficient.
Combining both statements gives the following equation: (7 + 2wf )(wp + 2wf ) − 7wp = 55,
where wp is the width of the photograph and wf is the width of the wooden frame.
Since there is one equation with two unknowns, it cannot be solved for wp unless the width of the frame is given. Thus, Statements (1) and (2) TOGETHER are NOT sufficient.
14. Is x < z?
(1) ax < az and a ≠ 0
(2) 14x < 14z
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) gives x < z (if a is positive) or x > z (if a is negative) on dividing both sides of the inequality by a. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives x < z on dividing both sides of the inequality by 14. Thus, statement (2) ALONE is sufficient.
15. What is the ratio of b to g?
(1) 4b + 2g = 18
(2) 4b = (8/5)g
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.If b : g is the required ratio, b / g needs to be found.
Statement (1) gives 4b + 2g = 18, which cannot be solved for b / g. Thus, statement (1) ALONE is not sufficient.
Statement (2) simplifies to b = (2/5)g, which implies b : g is 2 : 5. Thus, statement (2) ALONE is sufficient.
Try the Quiz : GMAT Test Prep : Quantitative Math Data Sufficiency Test III
|