|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
Is the data given in the two statements, labeled (1) and (2), sufficient for answering the question?
All numbers used are real numbers. |
1. Is positive integer a even?
(1) a is a multiple of 4.
(2) a is a factor of 44 × 22.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.Statement (1) specifies that a is a multiple of 4, and all multiples of 4 are even. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies that a is a factor of 44 × 22, but a could be odd (1) or even (2, 4, ...). Thus, statement (2) ALONE is not sufficient.
2. What percentage of the gloves manufactured at a factory are defective?
(1) The total number of gloves produced is 220.
(2) The ratio of defective gloves to non-defective gloves is 1 : 10.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies the total number of gloves, but does not specify the number of defective gloves to find the required percentage. Thus, statement (1) ALONE is not sufficient.
Statement (2) implies that the percentage of defective gloves is (1 / 11) x 100. Thus, statement (2) ALONE is sufficient.
3. What is the value of odd integer s?
(1) 1 < s < 10 .
(2) √s is also an odd integer.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) tells us that s = 3, or s = 5, or s = 7, or s = 9. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies that the square root of s is also an odd integer, but there are many possibilities of s (1, 9, 25, 49, ...) that satisfy this criterion. Thus, statement (2) ALONE is not sufficient.
On combining both statements, the value of s is uniquely determined as 9 (since √9 = 3), because √3 and √5 and √7 are not odd integers. Thus, BOTH statements TOGETHER are sufficient.
4. What is the sum of x, y and z?
(1) x, y and z are even prime numbers.
(2) The average of x, y and z is 2.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Statement (1) specifies that x = y = z = 2 (because 2 is the only even prime number). So, x + y + z = 6. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies that (x + y + z) / 3 = 2. So, x + y + z = 6. Thus, statement (2) ALONE is sufficient.
5.
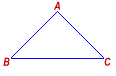
What is the perimeter of Δ ABC?
(1) AB = 10 inches
(2) AB = AC
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Perimeter of a triangle = Sum of lengths of the three sides; so, the lengths of AB, AC and BC must be known to calculate the perimeter.
Statement (1) specifies only the length of AB. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies that AB = AC, but nothing about their individual lengths. Thus, statement (2) ALONE is not sufficient.
Even when both statements are combined, we only know the lengths of AB and AC, but the length of BC is unknown. Thus, statements (1) and (2) TOGETHER are NOT sufficient.
6. The operator & represents which one of the following operations: addition, subtraction, multiplication or division?
(1) For all x, 3&x = x&3
(2) For all x, 2x&3x = 6x2
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) tells us that the operation is commutative. So, the operator & can represent addition or multiplication.
Thus, statement (1) ALONE is not sufficient.
Statement (2) indicates that the operator & represents multiplication.
Thus, statement (2) ALONE is sufficient.
7. If x is a positive number, what is 10% of x?
(1) Forty percent of (30/x) is less than 6.
(2) Ten percent of (50x) is 50.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies that 0.4 (30/x) < 6 or (2/x) < 1.
Multiplying both sides by x (a positive number), one obtains x > 2.
Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies that 0.1 (50x) = 50, which implies x = 10.
So, 10% of x is 1.
Thus, statement (2) ALONE is sufficient.
8.

What is the perimeter of rectangle PQRS?
(1) PQ = 8 feet
(2) Its diagonal is 10 feet.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.To find the perimeter of rectangle, its length and width must be known because
Perimeter of rectangle = 2(Length + Width).
Statement (1) specifies the length. To find the rectangle's perimeter, either its width or its diagonal must be known. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the diagonal. To find the rectangle's perimeter using the Pythagorean theorem, either its length or its width must be known. Thus, statement (2) ALONE is not sufficient.
Knowing the length as well as the diagonal of the rectangle allows us to calculate its width by the Pythagorean theorem, and subsequently its
perimeter. Thus, BOTH statements TOGETHER are sufficient.
9. An investor purchased a total of 8000 shares of stocks A and B at a total cost of $20000. How many shares of stock A did the investor
purchase?
(1) The investor purchased thrice as many shares of stock A as stock B.
(2) Stock A costs $3 and stock B costs $1.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.If NA is the number of shares of stock A, then (8000 − NA) is the number of shares of stock B.
If P denotes the price per share, then PA NA + PB (8000 − NA) = 20000.
Statement (1) specifies NA = 3 (8000 − NA), which may be solved to obtain NA = 6000. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies PA = 3 and PB = 1. Thus, 3 NA + (8000 − NA) = 20000, which may be solved to obtain NA = 6000. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
10. What is the circumference of the circle?
(1) The diameter of the circle is 8 inches.
(2) The area of the circle is 16π square inches.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.The circumference can be calculated if the radius r is known because
Circumference of a circle = 2πr.
Statement (1) specifies the diameter, which when halved gives the radius. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies the area of the circle as 16π. Since the area of a circle is given by πr2, one obtains r2 = 16 or r = 4 and circumference = 8π. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
11. What is the average of three consecutive odd positive integers?
(1) The product of the smallest integer and the middle integer is 783.
(2) The sum of the three consecutive odd integers is 87.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Statement (1) gives x(x − 2) = 783, where x is the middle integer as well as the average, since the smallest integer is (x − 2) and the greatest
integer is (x + 2). The quadratic equation can be solved for x (positive root). Thus, statement (1) ALONE is sufficient.
Statement (2) specifies the sum. On dividing the sum by 3, the average can be found. Thus, statement (2) ALONE is sufficient.
12. If p + q + r = 81, what is p2 + q2 + r2?
(1) The average of p, q and r is 27.
(2) p, q and r are positive consecutive odd integers.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies the average, which can be calculated from the question statement itself. There are many possibilities for p, q and r. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives p + (p + 2) + (p + 4) = 81,which can be solved for p. Then, q = p + 2 and r = p + 4. On adding the squares of the three
integers, the required value can be determined. Thus, statement (2) ALONE is sufficient.
13. Prospero is 15 years older than his brother Antonio. How old is Prospero?
(1) Twenty years ago, Prospero's age was twice that of Antonio.
(2) Ten years later, Antonio's age will be ¾ that of Prospero.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.The question statement gives p = a + 15,
where p is Prospero's present age and a is Antonio's present age.
Statement (1) gives p − 20 = 2(a − 20) or p − 20 = 2(p − 35), which may be solved to obtain p = 50. Thus, statement (1) ALONE is sufficient.
Statement (2) gives ¾(p + 10) = a + 10 or 3(p + 10) = 4(p − 5), which may be solved to obtain p = 50. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
14. 'The Fruit Mart' sells packets of mixed fruits. One packet of mixed fruits contains ¼ pound of apples, ½ pound of grapes and ¾ pound of bananas. What is the cost of one packet of mixed fruits?
(1) One pound of apples, grapes and bananas costs $2.49, $2.99 and $0.99 respectively.
(2) One pound of apples costs $0.50 less than one pound of grapes, and $1.50 more than one pound of bananas.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.To find the cost of one packet of mixed fruits, the costs of apples, grapes and bananas must be known.
Statement (1) specifies the unit costs of apples, bananas and grapes (per pound). When multiplied by their respective weights and added, the required cost of one packet of mixed fruits is obtained. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies only the relation between the costs of apples and grapes, and the relation between the costs of apples and bananas. The actual numerical value of the unit cost of one of the fruits is required. Thus, statement (2) ALONE is not sufficient.
15. Is integer n positive?
(1) mn < 0
(2) m > 0
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) states that mn < 0, which implies that n may be positive (if m is negative) or n may be negative (if m is positive). Thus, statement (1) ALONE is not sufficient.
Statement (2) states that m is positive, but nothing about n. Thus, statement (2) ALONE is not sufficient.
Combining both statements, m is positive as per statement (2) and consequently n must be negative as per statement (1). Although the answer to the question "is integer n positive?" is "no", it must be emphasized that the data is sufficient to provide a definite answer to the question. Thus, BOTH
statements TOGETHER are sufficient.
Try the Quiz : GMAT Test Prep : Quantitative Math Data Sufficiency Test IV
|