|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
Is the data given in the two statements, labeled (1) and (2), sufficient for answering the question?
All numbers used are real numbers. |
1. Is −x < (1/x) ?
(1) x < −1
(2) |x| > 0
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.Statement (1) specifies that x < −1, which implies −x > 1, −1 < (1/x) < 0 and −x > (1/x).
Thus, statement (1) ALONE is sufficient.
Statement (2) specifies that |x| > 0, which implies x > 0 or x < 0.
If x > 0, then −x is negative, (1/x) is positive and −x < (1/x).
If x < 0, then −x is positive, (1/x) is negative and −x > (1/x).
Thus, statement (2) ALONE is not sufficient.
2. 'The Olive Shop' sells only bottles of green olives and black olives. If 90 bottles of black olives and 40 bottles of green olives are sold on an average daily, what is the shop's average daily income?
(1) The price of a bottle of black olives is the same as that of a bottle of green olives.
(2) The price of 9 bottles of black olives and 4 bottles of green olives together is $26.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies that the price of both types of olives is the same, but does not give a numerical value for the price. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives the following equation:
9b + 4g = 26,
where bis the price of a bottle of black olives and g is the price of a bottle of green olives.
Note that when this equation is multiplied by 10 throughout, the price of 90 bottles of black olives and 40 bottles of green olives is obtained. Thus, statement (2) ALONE is sufficient.
3.
What is the area of Δ ABC?
(1) Δ ABC is isosceles.
(2) AB= 10 and BC = 12
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) only tells us that Δ ABC is isosceles which is not enough to find the area of the triangle. Thus, statement (1) ALONE is not sufficient. Statement (2) specifies the length of the base, but does not specify the altitude (or height) of the triangle. Thus, statement (2) ALONE is not sufficient. 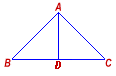 In an isosceles triangle, the altitude from the vertex angle bisects the base (as shown in the figure alongside). So, BD = ½ BC. Knowing ABand BD, the altitude AD can be found by the Pythagorean theorem. Since area of triangle = ½ base x altitude, the area can be determined as ½ BC x AD. Thus, BOTH statements TOGETHER are sufficient.
4.
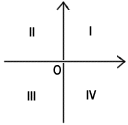
In which of the four quadrants of the rectangular coordinate system in the figure above does the point (x, y) lie ?
(1) x + 2y = −13 and 2x + y = −11
(2) x< −2 and y < −4.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.The quadrant in which the point lies can be determined if the sign (+ or −) of both xand y are known.
Statement (1) gives two linear equations that may be solved to determine the values of the two unknowns xand y.Thus, statement (1) ALONE is sufficient.
Statement (2) specifies the sign of both xand y to be negative. So, the point is in quadrant III. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
5. A clothing store sells only shirts and trousers. How much money did it collect from shirt sales on a particular day?
(1) Each shirt was sold for $14.99.
(2) It sold shirts and trousers in the ratio 4 : 1 on that day.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Statement (1) specifies the price of each shirt, but not the number of shirts sold. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the ratio of shirts to trousers, but nothing about their numbers. Thus, statement (2) ALONE is not sufficient.
The money collected from shirt sales can be found on multiplying the price per shirt by the number of shirts. Since the number of shirts sold cannot be obtained, statements (1) and (2) TOGETHER are NOT sufficient.
6.
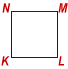
What is the perimeter of square KLMN?
(1) KL = 4 inches
(2) Its diagonal is √32 inches.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.To find the perimeter of square, its side must be known because
Perimeter of square = 4 × Side.
Statement (1) specifies the side. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the diagonal. The side of the square may be found using the Pythagorean theorem and then the perimeter calculated as follows:
KL2 + LM2 = (√32)2
Since KL = LM, 2LM2 = 32 or LM = √16 = 4 inches.
Perimeter of square = 4 × 4 inches = 16 inches.
Thus, statement (2) ALONE is sufficient.
7. In the rectangular coordinate system, is the point (m, n) farther from the origin than point (p, q)?
1) mn − pq = 12
(2) p + q = 21.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Distance of point (m, n) from origin = m2 + n2
Distance of point (p, q) from origin = p2 + q2
Difference in distances = (m2 + n2) −(p2 + q2)
= (m + n)2 − 2mn −(p + q)2 + 2pq
= (m + n)2 − (p + q)2 − 2(mn − pq)
Statement (1) specifies (mn − pq), whereas statement (2) specifies (p + q). Since there is no information available on (m + n), statements (1) and (2)
TOGETHER are NOT sufficient.
8. A company prepares a consignment by packing 20 compact discs in each small box. If the same consignment was to be packed in big boxes with 50 discs in each box, how many big boxes would be required ?
(1) The consignment is for a total of 6000 compact discs.
(2) The ratio of the number of big boxes to the number of small boxes is 2 : 5.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.Let sand b be the number of small and big boxes, respectively.
Then, total number of discs t = 20s = 50b.
Statement (1) specifies t = 6000, which gives b = 6000/50.Thus, statement (1) ALONE is sufficient.
Statement (2) specifies b/s = 2/5; however, this information is already known from 20s = 50b. Thus, statement (2) ALONE is not sufficient.
9. In 2000 the value of televisions sold constituted 23.4 percent of the goods sold by an electronics store that year. By what percent did the value of televisions sold annually by the electronics store change from 2000 to 2004 ?
(1) In 2004 the value of televisions sold constituted 17.8 percent of the goods sold by the electronics store that year.
(2) The ratio of the value of goods sold by the electronics store in 2000 to that in 2004 is 9/10.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Let Tand G denote the values of televisions and goods, respectively.
Then, T2000 = 0.234 G2000.
Required percent change = (1 − T2004/T2000) x 100%
Statement (1) gives T2004 = 0.178 G2004. Without knowing the values of G2000and G2004, the required percent change cannot be determined. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies G2000/G2004= 9/10. Without knowing the value of T2004, the required percent change cannot be found. Thus, statement (2) ALONE is not sufficient.
On combining both statements, the required percent change = [1 − (0.178 G2004)/(0.234 G2000)] x 100% = [1 − (0.178 x 10)/(0.234 x 9)] x 100%. Thus, BOTH statements TOGETHER are sufficient.
10. If xy ≠ 0, n = x/y, and d = 3/(4y) + 4/(3y), then what is the value of n/d ?
(1) x = 2
(2) y = 2x
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.Now, d = 3/(4y) + 4/(3y) = 9/(12y) + 16/(12y) = 25/(12y).
n/d = x/y × 12y/25 = 12x/25.
Statement (1) specifies the value of x, which allows determination of n/d. Thus, statement (1) ALONE is sufficient.
Statement (2) states that y = 2x. Without the explicit value of x, the quantity n/d cannot be determined. Thus, statement (2) ALONE is not sufficient.
11.
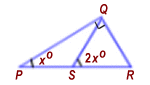
What is the length of side RS in the right-angled triangle PQR in the figure above ?
(1) x = 30
(2) Line segment PS has length 5.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.From the figure, ∠ PSQ measures (180 − 2x)o. Since the angles of the triangle PSQ must add to 180o, ∠ PQS must measure xo. Thus, PQS is an isosceles triangle with PS = QS.
In the figure, ∠ PQR measures 90o. Since ∠ PQS measures xo, ∠ RQS measures (90 − x)o. Now, the angles of the triangle RQS must add to 180o; so, ∠ QRS must measure (90 − x)o. Thus, RQS is an isosceles triangle with RS = QS.
It may be therefore concluded that RS = QS = PS.
Statement (1) specifies ∠ QPS; however, the above analysis shows that the actual numerical value of the angle is not required to determineRS. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies PS, and RS = PS from the preceding analysis. Thus, statement (2) ALONE is sufficient.
12.
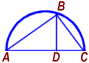
If arc ABC in the figure above is a semicircle and line segment BD has length 6, what is the length of diameter AC ?
(1) Line segment AB has length 10
(2) Line segment BC has length 7.5
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Using the Pythagorean Theorem for right-angled triangle ABD gives
AB2 = AD2 + BD2 ...(1)
Using the Pythagorean Theorem for right-angled triangle BCD gives
BC2 = BD2 + CD2 ...(2)
Note that an angle inscribed in a semicircle is a right angle. Since AC is a diameter, ∠ ABC measures 90o and ABC is a right-angled triangle.
Using the Pythagorean Theorem for right-angled triangle ABC gives
(AD + CD)2 = AB2 + BC2 ...(3)
Expanding the left-hand side above, and substituting from equations (1) and (2) into the right-hand side gives
AD2 + CD2 + 2 AD CD =AD2 + BD2 + BD2 + CD2 ...(4)
Simplifying equation (4) gives
AD CD = BD2 ...(5)
Statement (1) specifies AB. Since BD is given in the question statement, AD may be first calculated from equation (1) and then CD from equation (5). The diameter AC is simply the sum of ADand CD. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies BC. Since BD is given in the question statement, CD may be first calculated from equation (1) and then AD from equation (5). The diameter AC is simply the sum of CDand AD. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
13.

In the triangle ABC in the figure above, ∠ B measures 36o. How much does ∠ A measure ?
(1) ∠ B = ∠ C
(2) AB = AC
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Since the angles of a triangle add to 180o, ∠ A + ∠ B + ∠ C = 180o.
Statement (1) states that ∠ B = ∠ C. Since∠ B = 36o, ∠ A may be calculated from∠ A = 180o − 2 ∠ B. Thus, statement (1) ALONE is sufficient.
Statement (2) states that two sides of the triangle are equal in length,which implies the triangle is isosceles with ∠ B = ∠ C.As before, given ∠ B = 36o, ∠ A may be calculated from ∠ A = 180o − 2 ∠ B.Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
14. If the number of eligible voters is 160000, how many eligible voters did not vote ?
(1) 44 percent of the eligible women did not vote.
(2) 63 percent of the eligible men voted.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Let Mand W denote the number of men and women, respectively. Further, let subscripts V and N denote those who voted and those who did not vote, respectively. Then, MV + WV + MN + WN = 160000, and what is required is MN + WN.
Statement (1) states that WN = 0.44 (WN + WV), which yields WV = (0.56/0.44) WN. Thus, statement (1) ALONE is not sufficient.
Statement (2) states that MV = 0.63 (MV + MN), which yields MV = (0.63/0.37) MN. Thus, statement (2) ALONE is not sufficient.
On combining both statements, one obtains (1 + 0.63/0.37)MN + (1 + 0.56/0.44)WN = 160000. It is still not possible to evaluate (MN + WN) without knowing the value of at least one more variable. Thus, statements (1) and (2) TOGETHER are NOT sufficient.
15. David and Harry together weigh 260 pounds. How much does David weigh ?
(1) Harry's weight is 1½ times David's weight.
(2) Harry is 52 pounds more in weight than David.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Let D and H denote David's weight and Harry's weight, respectively. Then, it is given that D + H = 260.
Statement (1) states that H = 1.5 D, which may be used to eliminate H and solve for D. Thus, statement (1) ALONE is sufficient.
Statement (2) states that H = D + 52, which may be independently used to eliminate H and solve for D. Thus, statement (2) ALONE is sufficient.
Therefore, EACH statement ALONE is sufficient.
Try the Quiz : GMAT Test Prep : Quantitative Math Data Sufficiency Test V
|