|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
Is the data given in the two statements, labeled (1) and (2), sufficient for answering the question?
All numbers used are real numbers. |
1. A building has two types of apartments, big and small. 65 percent of the apartments are small. The number of occupied big apartments is twice the number of unoccupied small apartments. What percent of the apartments in the building are occupied ?
(1) The number of occupied big apartments is six times the number of unoccupied big apartments.
(2) The building has a total of 160 apartments.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.If 65% of the apartments are small, then 35% are big. Statement (1) specifies the ratio of occupied to unoccupied in big apartments is 6:1. This implies that 30% of the building is occupied big apartments. Since it is given that the number of occupied big apartments is twice the number of unoccupied small apartments, 15% of the building is unoccupied small apartments. If 65% of the building is small apartments, then 50% is occupied small apartments. Adding 30% (for occupied big apartments) to 50% (for occupied small apartments) gives 80% for the occupied apartments in the building. Thus, statement (1) ALONE is sufficient.
Statement (2) ALONE is insufficient because the question pertains to percent occupancy, where the actual number of apartments is irrelevant as demonstrated through equations below.
Let S denote the number of small apartments, B the number of big apartments and T the total number of apartments. Further, let subscripts O and U denote occupied and unoccupied. Then, the following equations can be formulated.
SO + SU = 0.65 T (given)
BO + BU = 0.35 T (given)
BO = 2 SU (given)
BO = 6 BU (Statement 1)
The above four equations can be solved to obtain SO and BO in terms of T, and then calculate the required occupancy percent from (SO + BO)/T.
Clearly, the value of T = 160 as given in Statement (2) is not required.
2. A pipe of length 100 inches is cut into three pieces of unequal lengths. What is the length of the longest piece?
(1) The combined length of the two longer pieces is 80 inches.
(2) The combined length of the two shorter pieces is 50 inches.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Let the lengths of the three pieces be given by x, y and z inches respectively (in ascending order of lengths).
Then, x + y + z = 100. To answer the question, z is required.
Statement (1) gives y + z = 80, which implies x = 20. Given the combined length of the two longer pieces and the total pipe length, the length of the shortest piece can be found. However, the length of the longest piece cannot be determined. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives x + y = 50, which implies z = 50. Given the combined length of the two shorter pieces and the total pipe length, the length of the longest piece can be determined. Thus, statement (2) ALONE is sufficient.
3. A certain electronics store sold 60 percent of the computers in its inventory during the month. What was the total revenue from the sale of the computers?
(1) The computers were sold for an average price of $875 during the month.
(2) All but 34 computers in the store's inventory were sold during the month.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) specifies the average price, but not the number of computers sold. Thus, statement (1) ALONE is not sufficient.
Statement (2) allows calculation of the number of computers sold, but not the price. Thus, statement (2) ALONE is not sufficient.
Since 34 computers are left (which corresponds to 40% of the inventory), the inventory may be calculated (as 85). Then, 60% of this inventory may be multiplied by the average price to obtain the total revenue. Thus, BOTH statements TOGETHER are sufficient.
4. Is a greater than 0 ?
(1) ab < 0 and a − b < 0.
(2) ac > 0 and c < 0.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.Statement (1) states that ab < 0, which implies that either a or b is negative and the other is positive. Further, a < b implies that a is negative and b is positive. Thus, statement (1) ALONE is sufficient (to answer the question in the negative).
Statement (2) states that ac > 0, which implies that either botha and c are positive or both are negative. Further, c < 0 implies that both a and c are negative. Thus, statement (2) alone is sufficient (to answer the question in the negative).
Therefore, EACH statement ALONE is sufficient.
5. Train A travels from Town P to Town Q, while Train B travels from Town Q to Town P. Both trains start at the same time. Town R lies between Town P and Town Q. Which train travels at a higher speed?
(1) Town R lies closer to Town P than Town Q.
(2) Train A crosses Town R earlier than Train B does.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Note that Speed = Distance traveled / Time taken.
Statement (1) provides some information on the distance traveled, but nothing about the time taken. So, statement (1) ALONE is not sufficient.
Statement (2) provides some information on the time taken, but nothing about the distance traveled. So, statement (2) ALONE is not sufficient.
Even both statements together cannot tell us which train travels faster because of the following argument. If Train A travels faster than Train B, it will certainly cross Town R earlier than Train B does. But, even if Train A travels slower than Train B, and if Town R lies very close to Town P, then Train A will still cross Town R before Train B does. Thus, statements (1) and (2) TOGETHER are not sufficient.
6.
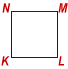
What is the area of square KLMN?
(1) KL = 7 inches.
(2) Its diagonal is √98 inches.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: EACH statement ALONE is sufficient.To find the area of square, its side must be known because
Area of square = Side × Side.
Statement (1) specifies the side. Thus, statement (1) ALONE is sufficient.
Statement (2) specifies the diagonal. The side can be found using the Pythagorean theorem and then the area calculated as follows:
KL2 + LM2 = (√98)2
Since KL = LM, 2LM2 = 98 or LM = √49 = 7 inches.
Area of square = 7 × 7 square inches = 49 square inches.
Thus, statement (2) ALONE is sufficient.
7. Every month, Michael gets a salary plus a commission equal to 2 percent of his sales revenue. What was Michael's commission for the month of January?
(1) Michael's monthly salary is $1,750.
(2) Michael's sales revenue for the month of January was $2,750.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) specifies the monthly salary, which does not pertain to the commission. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the sales revenue for the month of January, and a fixed percentage of this revenue is the commission. Thus, statement (2) ALONE is sufficient.
8. Is the integer n divisible by 30 ?
(1) n is divisible by 18.
(2) n is divisible by 20.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.If an integer is divisible by 18, it may or may not be divisible by 30. For example, 36 is divisible by 18 but not by 30, whereas 90 is divisible by 18 as well as 30. Thus, statement (1) ALONE is not sufficient.
If an integer is divisible by 20, it may or may not be divisible by 30. For example, 40 is divisible by 20 but not by 30, whereas 60 is divisible by 20 as well as 30. Thus, statement (2) ALONE is not sufficient.
If an integer is divisible by both 18 and 20, then it is necessarily divisible by 30. Since 18 = 2 × 3 × 3 and 20 = 2 × 2 × 5, their LCM (least common multiple) is 180 = 2 × 2 × 3 × 3 × 5. Multiples of 180 are divisible by 30. Thus, BOTH statements TOGETHER are sufficient.
9. Is m an integer?
(1) 4m is an integer.
(2) m/4 is an integer.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.If 4m is an integer, m may or may not be an integer. For example, 4m = 5 gives m = 5/4 = 1.25, whereas 4m = 8 gives m = 2. Thus, statement (1) ALONE is not sufficient.
If m/4 is an integer (say, n), then m is necessarily an integer (namely, 4n). Thus, statement (2) ALONE is sufficient.
10. What number is ¾ of y ?
(1) 5 percent of x and 15 percent of y total 8.
(2) One-tenths of x and three-tenths of y equal 16.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Statement (1) gives 5x + 15y = 800. Two unknowns cannot be determined from one equation. Thus, statement (1) ALONE is not sufficient. Statement (2) gives x + 3y = 160. Again, two unknowns cannot be determined from one equation. Thus, statement (2) ALONE is not sufficient.
The two equations are not independent because multiplying x + 3y = 160 throughout by 5 gives 5x + 15y = 800. Thus, statements (1) and (2) TOGETHER are NOT sufficient.
11. A terminating decimal is defined as any decimal that has a finite number of nonzero digits. When the ratio of two positive integers m and n is expressed as a decimal, is m/n a terminating decimal?
(1) 330 < m < 333
(2) n = 3
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) states that m is either 331 or 332. Now, 332/2 (= 166) is a terminating decimal, but 332/3 (= 110.666...) is a recurring decimal (and not a terminating decimal). Thus, statement (1) ALONE is not sufficient.
Statement (2) states that n is 3. If m is a multiple of 3, then m/n is a terminating decimal; otherwise, it is a recurring decimal (ending in .333... or .666...). Thus, statement (2) ALONE is not sufficient.
If m is either 331 or 332 and n is 3, then m/n is necessarily a recurring decimal. Since 331/3 = 110.333... and 332/3 = 110.666..., m/n is not a terminating decimal. Thus, BOTH statements TOGETHER are sufficient.
12. How long will it take to fill an empty tank of circular cross-section with a certain liquid?
(1) The tank is 1.5 feet in radius and 3 feet in height.
(2) Liquid is pumped in at the rate of 4 gallons per hour (1 cubic foot = 7.48 gallons).
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.Statement (1) specifies the radius (say, r) and height (say, h). Although the volume of the tank can be calculated (from the formula: Volume of cylinder = π r2h), the time to fill the tank cannot be found without knowing the flow rate. Thus, statement (1) ALONE is not sufficient.
Statement (2) specifies the flow rate, but the time to fill the tank cannot be calculated without knowing the tank volume. Thus, statement (2) ALONE is not sufficient.
Knowing the volume from statement (1) and the flow rate from statement (2), the time to fill the tank can be calculated from the formula:
Time = Volume / Flow rate.
Thus, BOTH statements TOGETHER are sufficient.
13. Is x negative ?
(1) x2 > 0
(2) x3 > 0
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Statement (1) states that the square of the number x is positive, which implies that x may be positive or negative. Thus, statement (1) ALONE is not sufficient.
Statement (2) states that the cube of the number x is positive, which necessarily implies that x is necessarily positive (and not negative). Thus, statement (2) ALONE is sufficient.
14. A fruit basket contains only apples, bananas and peaches. If a fruit is chosen at random from the fruit basket, what is the probability that it will be a peach ?
(1) The probability that the fruit will be a banana is ½.
(2) There are 7 peaches in the fruit basket.
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statements (1) and (2) TOGETHER are NOT sufficient.Let a, b and p denote the number of apples, bananas and peaches, respectively. Then, the probability of choosing a peach may be calculated from p/(a + b + p).
Statement (1) gives b/(a + b + p) = ½ or b = a + p. Then, the probability of choosing a peach becomes p/(2b), which cannot be evaluated further. Thus, statement (1) ALONE is not sufficient.
Statement (2) gives p= 7. Then, the probability of choosing a peach becomes 7/(a + b + 7), which cannot be evaluated further. Thus, statement (2) ALONE is not sufficient.
On combining both statements, the probability of choosing a peach becomes 7/(2b) which also cannot be evaluated further. Thus, statements (1) and (2) TOGETHER are NOT sufficient.
15. If p is less than 80 percent of q, is q greater than 80 ?
(1) 4q − 5p > 0
(2) p > 64
• Statement (1) ALONE is sufficient, but statement (2) ALONE is not sufficient.
• Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.
• BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
• EACH statement ALONE is sufficient.
• Statements (1) and (2) TOGETHER are NOT sufficient.
Answer: Statement (2) ALONE is sufficient, but statement (1) ALONE is not sufficient.Since p < 0.8q and 0.8 = 4/5, q > (5/4)p.
Statement (1) states that 4q > 5p, which implies that q > (5/4)p. Since there is no new information here, Statement (1) ALONE is not sufficient. Statement (2) states that p > 64. So, (5/4)p > 80 or q > 80. Thus, statement (2) ALONE is sufficient.
Try the Quiz : GMAT Test Prep : Quantitative Math Data Sufficiency Test VI
|