|
Hide all answers
Hide all answers
View all answers
View all answers
Print
Try the Quiz
| Compare the two quantities and choose the best answer from four choices given. |
1.
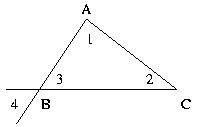
Diagram is illustrative and is not drawn to scale.
Quantity A = Measure of angle 1 + Measure of angle 4
Quantity B = 90o - Measure of angle 2o
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterIn the figure, angles 3 and 4 are vertically opposite angles and are equal.
Also the sum of the three angles of a triangle is 180o.
Hence angle 1 + angle 2 + angle 4 = 180o or
angle 1 + angle 4 = 180o - angle 2.
2. Quantity A = (27 - 13) (296 + 534) Quantity B = (27 + 13) (534 + 296)
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterLet y = 296 + 534.
Then, Quantity A = 14y and Quantity B = 40y. Now, 14y < 40y.
Note that you save time by not calculating the exact values of Quantity A and Quantity B.
3. y2 + z2 = 34 and yz = 15
Quantity A = y2 + 2yz + z2
Quantity B = (y + z)2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalIt is worth remembering that
(y + z)2 = (y + z) (y + z) = y2 + 2yz + z2
Note that it is not meaningful to solve the equations simultaneously and determine y and z equal +3 or -3 and +5 or -5.
4. Quantity A = (y + 5)2 Quantity B = (y - 5)2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The relationship cannot be determined from the information givenFor y = 0, (y + 5)2 = (y - 5)2 = 25
For y < 0, (y + 5)2 < (y - 5)2
For y > 0, (y + 5)2 > (y - 5)2
5. Quantity A = (1/25)1/2 + (1/144)1/2 Quantity B = [(1/25) + (1/144)]1/2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greater(1/25)1/2 + (1/144)1/2 = (1/5) + (1/12) = 17/60.
[(1/25) + (1/144)]1/2 = [(144+25) / (25 x 144)]1/2 = [169/(25 x 144)]1/2 = 13/60.
6. Quantity A = Time to travel 95 miles at 50 miles per hour
Quantity B = Time to travel 125 miles at 60 miles per hour
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterTime = Distance / Speed
Time to travel 95 miles at 50 miles per hour = 95/50 < 2 hours.
Time to travel 125 miles at 60 miles per hour = 125/60 > 2 hours.
Note that you save time by not calculating the exact values of Quantity A and Quantity B.
7. Quantity A = 4 / 100 Quantity B = 0.012 / 3
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greater4/100 = 0.04 and 0.012/3 = 0.004. Note that 0.04 > 0.004
8. Quantity A = 1.1 Quantity B = 12.11/2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterNow 91/2 = 3 and 161/2 = 4.
So, 12.11/2 lies between 3 and 4. Therefore, it is greater than 1.1
Note that you save time by not calculating the exact values of Quantity A and Quantity B.
Also, note that 1.12 = 1.1 x 1.1 = 1.21 (and not 12.1).
9. Quantity A = (9/13)2 Quantity B = (9/13)1/2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterA tricky problem.
Let y = 9/13. However, it is not meaningful to try to manually calculate y2 or y1/2 in this case. The relationship is not indeterminate because the
uantities are given numbers. It is also clear that Quantity A does not equal Quantity B here.
So, we need to ascertain whether y2 is greater than or less than y1/2
when 0 < y < 1.
Note y2 < y when 0 < y < 1.
Also y1/2 > y when 0 < y < 1.
Therefore, y1/2 > y2 when 0 < y < 1... worth remembering!
10. Quantity A = 0.83 Quantity B = 0.81/3
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterA tricky problem.
Let y = 0.8 ; however, it is not meaningful to try to manually calculate y3 or y1/3 in this case. The relationship is not indeterminate because the
uantities are given numbers. It is also clear that Quantity A does not equal Quantity B here.
So, we need to ascertain whether y3 is greater than or less than y1/3
when 0 < y < 1.
Note y3 < y when 0 < y < 1.
Also y1/3 > y when 0 < y < 1.
Therefore, y1/3 > y3 when 0 < y < 1... worth remembering!
11. Quantity A = (3 x 4 x 17) / (121 x 100)
Quantity B = (4 x 5 x 19) / (1000 x 121)
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterLet y = 4/121.
Then, Quantity A = (3 x 17)/(100 y) = 0.51 y and
Quantity B = (5 x 19)/(1000 y) = 0.095 y. Now, 0.51 y > 0.095 y.
Note that you save time by not calculating the exact values of Quantity A and Quantity B.
12. 100 < y < 200 and 100 < z < 210
Quantity A = y Quantity B = z
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The relationship cannot be determined from the information givenThe relationship is clearly indeterminate because y can take any value between 100 and 200, whereas z can take any value between 100 and 210.
hus, y = z, y < z or y > z.
13. Consider a triangle PQR.
Quantity A = length of PQ + length of QR
Quantity B = length of PR
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterWith some visualization, it is clear than PQ + QR can never be less than or equal to PR. In fact, the sum of the lengths of two sides (PQ + QR) is
ecessarily greater than the length of the third side PR.
14. Consider a rectangle. The length of its shorter side is 8, and the length of its diagonal is 16.
Quantity A = 30o
Quantity B = measure of angle formed by diagonal and shorter side
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterA rough sketch will help in visualizing the solution.
The diagonal with the two sides of the rectangle forms a right triangle.
The measure of the angle formed by the diagonal and the shorter side is 60o because cos 60o = 1/2 = 8/16. So, Quantity B = 60o
15. Quantity A = Percentage increase from 10 ft to 13 ft
Quantity B = Percentage increase from 13 ft to 16 ft
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterQuantity A = (3/10) x 100 and Quantity B = (3/13) x 100. Now, 3/10 > 3/13.
Note that you save time by not calculating the exact values of Quantity A and Quantity B.
16. Quantity A = Time elapsed from 6:47 a.m. to 10.13 the same morning
Quantity B = 3 hours 25 minutes
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterQuantity A = 3 hours 26 minutes (on adding up
13 minutes from 6.47 a.m. to 7 a.m.,
3 hours from 7 a.m. to 10 a.m., and again
13 minutes from 10 a.m. to 10.13 a.m.)
17. Quantity A = Volume of a cube in which the length of a side is 5
Quantity B = Volume of a cube in which the length of a diagonal of a face is 6 (2)1/2
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterIf side = 5, then volume of cube = 53 = 125.
If side = a, then diagonal of a face = (a2 + a2)1/2 = (2)1/2 a.
If diagonal of a face = 6 (2)1/2, then side = 6 and volume = 63 = 216.
Note that you may save time by not calculating the volumes. If the side of the cube is greater in length, then its volume must be greater.
18. Quantity A = Average of (2y + 3z + 127) and (4y + 5z + 73)
Quantity B = Average of (3y + 4z + 173) and (3y + 4z + 73)
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity B is greaterQuantity A = (2y + 4y + 3z + 5z + 127 + 73)/2
= (6y + 8z + 200)/2 = 3y + 4z + 100.
Quantity B = (3y + 3y + 4z + 4z + 173 + 73)/2
= (6y + 8z + 246)/2 = 3y + 4z + 123.
19. A task is done by y women in 45 hours.
The same task is done by (y + 2) women in z hours.
Quantity A = 45 Quantity B = z
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: Quantity A is greaterIf the number of women is increased, then the task is done in fewer hours.
So, z < 45.
20.
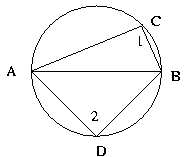
Diagram is illustrative and is not drawn to scale.
AB is the diameter of the circle.
Angle BAC = 30o
Quantity A = Length of side AB
Quantity B = 2 (Length of side BC)
• Quantity A is greater
• Quantity B is greater
• The two quantities are equal
• The relationship cannot be determined from the information given
Answer: The two quantities are equalAngle subtended by the diameter on the circumference = 90o.
So, ABC is a right triangle.
sin BAC = opposite side / hypotenuse = BC / AB.
sin BAC = sin 30o = 0.5
So, BC / AB = 0.5 or AB = 2 BC.
Try the Quiz : GRE Test Prep : Quantitative Comparison I
|