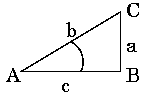Math : Trigonometry
|
Values of Trigonometric Functions for Common AnglesIt is useful to know the values of the trigonometric functions for certain common angles. The values of the trigonometric functions for angles 0, 30o, 45o, 60o and 90o are given in the table below.
It is possible to obtain the values in the above table for 0, 45o and 90o by using the definitions from Trigonometry Module 1.
The values in the above table can be easily remembered using the following mnemonic. The values of sin 0, sin 30o, sin 45o, sin 60o and sin 90o are simply given by the square roots of 0/4, 1/4, 2/4, 3/4 and 4/4. The values of cos 0, cos 30o, cos 45o, cos 60o and cos 90o are given by the square roots of 4/4, 3/4, 2/4, 1/4 and 0/4. Obviously, the values of tan for any angle are obtained by dividing the sine value by the cosine value. Important Trigonometric IdentitiesSome important trigonometric identities relating functions of a single angle (say, A) are given below.
These identities are useful in simplification and solution of problems. Their proofs are given below.
Cofunction PropertyThe cofunction property is very important and is given below.
The cofunction property is easy to prove by starting with the fact that the sum of the three angles of a triangle is always 180o, i.e., A + B + C = 180o. For a right-angled triangle, angle B is 90o and A + C = 90o. On using 90o - C = A, the following are readily obtained:
Practice Exercise for Trigonometry Module 2: Trigonometric Functions and Identities |
5 more pages in Trigonometry