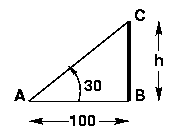Contents for Trigonometry Module 3: Word Problems on Heights and Distances
Trigonometry, in ancient times, was often used in the measurement of heights and distances of objects which could not be otherwise measured. For example, trigonometry was used to find the distance of stars from the Earth. Even today, in spite of more accurate methods being available, trigonometry is often used for making quick and simple calculations regarding heights and distances of far-off objects. For this, the value of various trigonometric functions is needed. A simple example is given below to demonstrate how trigonometry can help find the height or distance of an object.
If the distance of a person from a tower is 100 m and the angle subtended by the top of the tower with the ground is 30o, what is the height of the tower in meters?
Steps:
- Draw a simple diagram to represent the problem. Label it carefully and clearly mark out the quantities that are given and those which have to be calculated. Denote the unknown dimension by say h if you are calculating height or by x if you are calculating distance.
- Identify which trigonometric function represents a ratio of the side about which information is given and the side whose dimensions we have to find out. Set up a trigonometric equation.
- Substitute the value of the trigonometric function and solve the equation for the unknown variable.
Solution:
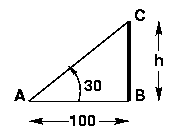
- AB = distance of the man from the tower = 100 m
- BC = height of the tower = h (to be calculated)
- The trigonometric function that uses AB and BC is tan A , where A = 30o.
| So tan 30o = BC / AB = h / 100 |
| Therefore height of the tower h = 100 tan 30o = (100) 1/√3 = 57.74 m. |
|
Most of the simple word problems in trigonometry can be solved by the method illustrated in the example above. Many questions on Heights and Distances in Trigonometry along with their solutions are available in the practice exercise.
Practice Exercise for Trigonometry Module 3: Word Problems on Heights and Distances